9465번 스티커
📝문제링크 : www.acmicpc.net/problem/9465
2차원 배열이 주어져 처음 보는 새로운 유형이라고 생각했는데, 결국 다른 DP 문제와 크게 다르진 않았다.
문제는 내가 혼자 풀이방법을 떠올리지 못한다는 것 ㅠㅠ
처음접근
인접한 스티커를 선택할 수 없으므로, n = 1 일 때 부터 대각선 방향만 고려하며 쌓아나아가 봤다. 그러나 한 칸을 건너 뛰고 다음 칸에서 스티커를 선택하는게 더 유리한 케이스도 있어, 1부터 쌓아나가는 방법으로는 답을 찾을 수 없었다.
- 정답보고접근
- 2차원 배열 dp 를 선언한다.
- $dp[i][j]$ 엔 $i$행 $j$열의 스티커를 선택했을 때 얻을 수 있는 최대값이 저장된다.
- $[j - 2]$ 인덱스와 $[j - 1]$ 인덱스 값을 비교해 더 큰 값을 취하고 현재 인덱스 값을 더한다. 그럼 한 칸을 건너 뛰어야 최대값을 구해지는 케이스까지 커버할 수 있다.
- 즉, 아래의 점화식으로 n열까지 답을 채워나가고 마지막열의 두 값 중 최대값을 선택하면 정답이 된다.
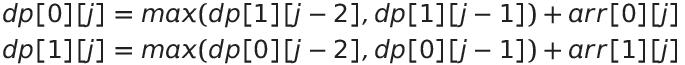
- $[j - 1]$ 인덱스 하나만 고려하지 않는 이유
인접한 스티커를 고를 수 없는 규칙 때문에, [j - 1] 값만 고려하면 선택지가 1개 뿐이게 된다.
- $[j - 1]$, $[j - 2]$, $[j - 3]$ 까지 3개의 인덱스를 고려하지 않는 이유
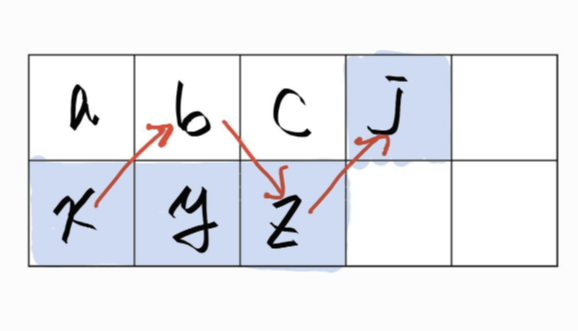
아래 그림을 보면, dp[0][j] 값을 결정할 땐, dp[1] 행의 데이터들을 고려한다.
3개의 값을 비교한 후 최대값으로 $x$가 선택되었다면, 아래 그림처럼 얼마든지 더 큰 값을 만들면서 $j$까지 갈 수 있기 때문에 j - 3번째 값은 고려하지 않아도 되는 것이다.
소스코드
|
#include <iostream>
#include <algorithm>
using namespace std;
int arr[2][100001]; //배열데이터가 저장됨
int dp[2][100001]; //최대값 정보가 저장됨
int main()
{
int T;
int n;
cin >> T;
for(int test_case = 0; test_case < T; test_case++)
{
//get_input
cin >> n;
for(int i = 0; i < 2; i++)
{
for(int j = 1; j < n + 1; j++)
{
cin >> arr[i][j];
}
}
//set initial value
dp[0][0] = 0;
dp[1][0] = 0;
dp[0][1] = arr[0][1];
dp[1][1] = arr[1][1];
//solve
//dp[i][j] 는 arr[i][j] 스티커를 선택했을 때의 최대값이다
for(int j = 2; j < n + 1; j++)
{
dp[0][j] = max(dp[1][j - 2], dp[1][j - 1]) + arr[0][j];
dp[1][j] = max(dp[0][j - 2], dp[0][j - 1]) + arr[1][j];
}
//result
cout << max(dp[0][n], dp[1][n]) << '\n';
}
return (0);
}
|
trivia
- 크기가 큰 배열을 사용할 땐, 전역으로 선언하지 않으면 메모리가 부족해 터질 수도 있다. 지역변수는 크기 제한이 있는 스택영역에 저장되기 때문이다. (전역변수는 data segment에 저장된다.) 일반적인 프로그래밍에선 전역변수의 사용을 지양하지만 알고리즘 풀이에서는 좀 더 유연하게 전역변수를 사용해도 될 것 같다.
- <algorithm> 의 max 함수를 처음 사용해봤다.
'알고리즘 > Problem Solving' 카테고리의 다른 글
| [BOJ] DP 11053 가장 긴 증가하는 부분수열 C++ (0) | 2020.12.28 |
|---|---|
| [BOJ] DP 2156 포도주 시식 C++ (0) | 2020.12.27 |
| [BOJ] DP 11057번 오르막 수 C++ (0) | 2020.12.04 |
| [BOJ] DP 10844번 쉬운 계단 수 C++ (0) | 2020.12.03 |
| [BOJ] DP 9095번 1, 2, 3 더하기 C++ (0) | 2020.11.24 |



